| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Spark 튜닝
- Oracle 논리적 저장 구조
- BFS
- enq: FB - contention
- git init
- Spark Data Read
- CF
- 데이터분석
- airflow 정리
- 랜덤포레스트
- Oracle ASSM
- git stash
- 알고리즘
- eda
- 데이터 분석
- 배깅
- 추천시스템
- 통계분석
- 의사결정나무
- 네트워크
- Spark jdbc parallel read
- 리눅스 환경변수
- git 기본명령어
- Decision Tree
- Collaborative filtering
- Linux
- 앙상블
- SQL
- 오라클 데이터 처리방식
- Python
- Today
- Total
[Alex] 데이터 장인의 블로그
데이터 분석을 위한 통계(ANOVA) feat. python 본문
ANOVA '쉽게' 기억하자
t-test(t-검정)에 이어서 ANOVA(분산분석) 대해 기억하기 쉽게 정리를 해보겠습니다.
t-검정에서는 A와 B 집단 딱 2개의 집단에 대한 차이를 비교할 수 있었다면 ANOVA 분석은 그보다 많은 집단의 차이를 비교할 수 있습니다.
세개 이상 집단 '평균'의 차이가 유의미한가?

ANOVA 분석(분산분석)은 '세 집단(or 이상)의 평균의 차이가 유의미한가'를 확인하기 위해 사용하는 분석 방법입니다. 또한 t-test와는 조금 다르게 ANOVA 분석은 개체간-분산과 개체내-분산을 이용하여 각 집단별 평균에 대한 유의성을 확인합니다. ANOVA 분석은 t-test 마찬가지로 등분산성, 정규성, 독립성의 조건이 전제되어야 합니다.
이전 T-TEST에서 사용했던 데이터를 그대로 가지고와서 분석을 진행해보겠습니다.
이전글: [데이터 분석을 위한 Statistic] - 데이터 분석을 위한 통계분석(t-test) feat. python
1. 데이터를 불러온뒤 JOIN 을 수행합니다.
import pandas as pd
import numpy as np
data = pd.read_csv("sales.csv", dtype = {'YMD' : 'object'})
wt = pd.read_csv("weather.csv")
# 날짜 데이터 변환
wt.tm = wt.tm.map(lambda x : x.replace('-', ''))
# DATA JOIN
DF = data.merge(wt, how='left', left_on = 'YMD', right_on = 'tm')
# 데이터 컬럼별 추출
data = DF.iloc[:,[0,2,7,8]]
data| YMD | CNT | MaxTa | SumRn |
| 20190514 | 1 | 26.9 | 0.0 |
| 20190519 | 1 | 21.6 | 22.0 |
| 20190521 | 4 | 23.8 | 0.0 |
| 20190522 | 7 | 26.5 | 0.0 |
| 20190523 | 13 | 29.2 | 0.0 |
| ... | ... | ... | ... |
| 20200424 | 51 | 14.3 | 0.0 |
| 20200425 | 34 | 17.1 | 0.0 |
| 20200426 | 55 | 19.0 | 0.0 |
| 20200427 | 45 | 18.3 | 0.0 |
| 20200428 | 45 | 19.9 | 0.0 |
2. 일별 최고온도 -> 구간 설정을 통해 연속형 변수를 명목형 변수로 바꿔줍니다.
data.maxTa.describe()
import matplotlib.pyplot as plt
ax = plt.boxplot(data.maxTa)
plt.show()
3. 최고, 최저 온도를 보고 제가 임의로 추움, 보통, 더움 (0,1,2)로 변수를 나누어 주겠습니다. (null 값 제외)
data['Ta_gubun'] = pd.cut(data.maxTa, bins=[-5,8,24,36], labels = [0,1,2])
data = data[data.Ta_gubun.notna()]4. 본격적인 검정에 앞서 간단히 상관분석을 진행해봅니다.
data.corr()
-> 매출건수와 온도간의 음의 상관관계가 보여지긴 하는군요.
5. 세 그룹으로 데이터를 나누어 준 뒤, 등분산 검정과 정규성 검정을 함께 수행합니다.
x1 = np.array(data[data.Ta_gubun == 0].CNT)
x2 = np.array(data[data.Ta_gubun == 1].CNT)
x3 = np.array(data[data.Ta_gubun == 2].CNT)from scipy import stats
# 등분산 검정
print(stats.bartlett(x1,x2,x3),stats.fligner(x1, x2, x3) ,stats.levene(x1, x2, x3), sep="\n")
# 정규성 검정
print(stats.ks_2samp(x1, x2), stats.ks_2samp(x1, x3), stats.ks_2samp(x3, x2), sep="\n")
spp = data.loc[:,['CNT','Ta_gubun']]
spp.groupby("Ta_gubun").count()
-> 등분산 검정은 바틀렛 검정으로 진행했을때만 조건 충족이 되었습니다. 등분산 조건을 만족할때와 아닐때 두 경우를 모두 살펴봐야 하겠습니다.
stats.ks_2samp : 콜모고로프-스미르노프 검정(Kolmogorov-Smirnov test)은 사실 정규분포에 국한되지 않고 두 표본이 같은 분포를 따르는지 확인할 수 있는 방법입니다.
6. ANOVA 분석을 진행합니다.
정규성 조건, 등분산성 조건 각각 충족하지 못하는 경우를 고려하여 추가분석도 진행하였습니다.
sp= np.array(spp)
group1 = sp[sp[: , 1]==0,0]
group2 = sp[sp[: , 1]==1,0]
group3 = sp[sp[: , 1]==2,0]
# df.boxplot(column = 'CNT', by = 'Ta_gubun', grid = False) : 간단히
plot_sp= [group1,group2, group3]
ax = plt.boxplot(plot_sp)
plt.show()
F_statistic, pVal = stats.f_oneway(group1, group2, group3)
print('데이터의 일원분산분석 결과 : F={0:.1f}, p={1:.10f}'.format(F_statistic, pVal))
print('데이터의 일원분산분석 결과 : F=%.2f , p=%.10f ' %(F_statistic, pVal))
-> 유의확률이 유의수준(0.05) 이하이므로 귀무가설 기각.
stats.kruskal(group1, group2, group3) #정규성 가정x Kruskal-Waliis test
-> 정규성 가정이 충족되지 않았을 때도 귀무가설 기각.
#등분산성 가정x Welch’s ANOVA
from pingouin import welch_anova
df = data
aov = welch_anova(dv='CNT', between='Ta_gubun', data=df)
aov 
-> 등분산성 가정을 만족하지 않았을 때도 귀무가설 기각.
해석:
날씨(추움, 보통, 더움)에 의해 매출건수의 차이가 유의미한 것으로 보여집니다. Box plot을 살펴보니 날씨가 더울수록 주문량이 낮아지는 것으로 보이네요. 더 자세히 살펴보기 위해 '사후분석'을 진행합니다.
7. 사후분석을 진행하여 그룹간 평균의 차이를 더욱 자세히 살펴봅니다.
from statsmodels.stats.multicomp import pairwise_tukeyhsd
posthoc = pairwise_tukeyhsd(spp['CNT'], spp['Ta_gubun'], alpha=0.05)
print(posthoc)
fig = posthoc.plot_simultaneous()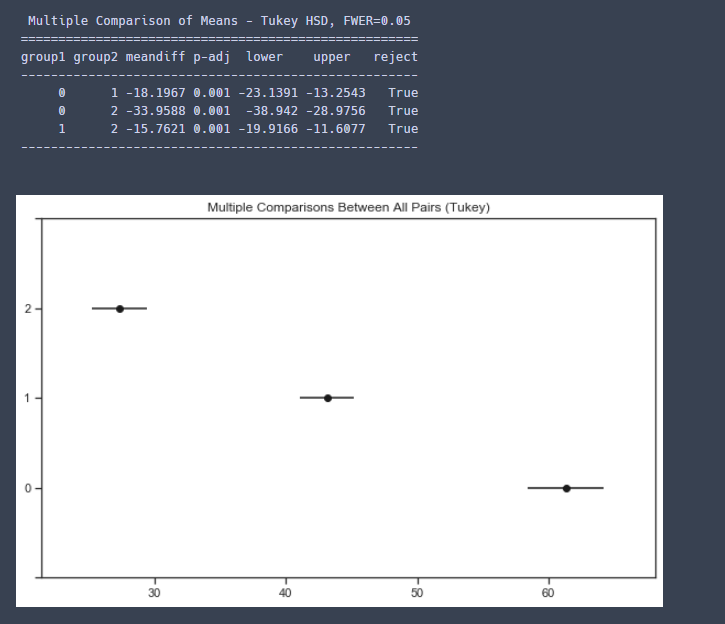
-> 각각 (더움-보통, 보통- 추움, 더움- 추움) 그룹 간 차이가 유의미하다고 보여지네요.
T-TEST에서 수행했던 분석과는 달리 온도에 따라서 배달량(주문량)의 차이가 발생하는 것으로 보여지네요.
흥미로운 결과이지만 이 결과를 곧이곧대로 해석하고 받아들이는 건 위험합니다. 단순히 '차이가 보여진다.' 라는 것이지 매출에 영향을 주는 요소는 온도 이외에도 엄청나게 많습니다. 차근차근 다른 변수들을 살펴보면서 매출에 영향을 끼치는 원인과 이에 따른 변화를 살펴보는 것이 중요합니다.
'Statistic' 카테고리의 다른 글
| 데이터 분석을 위한 통계(PCA - 주성분분석) feat.python (0) | 2020.06.14 |
|---|---|
| 데이터 분석을 위한 통계(카이스퀘어 검정) feat. python (2) | 2020.05.26 |
| 데이터 분석을 위한 통계(t-test) feat. python (2) | 2020.05.10 |



