| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Oracle ASSM
- 네트워크
- 데이터분석
- 랜덤포레스트
- 의사결정나무
- 리눅스 환경변수
- CF
- Decision Tree
- Spark 튜닝
- 통계분석
- Collaborative filtering
- Spark Data Read
- Oracle 논리적 저장 구조
- git init
- git 기본명령어
- Spark jdbc parallel read
- git stash
- BFS
- 추천시스템
- 배깅
- Linux
- 오라클 데이터 처리방식
- 데이터 분석
- SQL
- enq: FB - contention
- Python
- 알고리즘
- 앙상블
- eda
- airflow 정리
- Today
- Total
[Alex] 데이터 장인의 블로그
[Machine Learning] Decision Tree - 의사결정나무 본문
의사결정트리라고도 불리는 의사결정나무는 객체 레이블을 예측하는 매우 직관적인 방법이다. 단순히 입력 변수를 특정한 기준으로 잘라(분기) 트리 형태의 구조로 분류를 하는 모델이다.

보통 의사결정나무를 분석 모델로 선택하는 이유는 예측모형을 직접 보고 충분히 이해할 수 있기 때문이다.(속도가 빠른 것도) 로지스틱 회귀 등등 coef를 보고 해석할 수 있는 경우 있기야 하지만 의사결정 트리만큼 직관적이고 쉽게 해석할 수 있는 모델은 없다.
의사결정나무는 이진 분할을 통해 각 예측 Class 들의 옵션 수를 줄이고 때문에 빠르게 동작할 수 있다는 장점이 있다. 물론 각 단계마다 어떤 Feature에 어떤 질문을 하느냐가 중요하다. 어떤 질문을 하는지는 보통 불순도를 낮추는 방향이나 순수도를 높히는 방향으로 이루어진다. (결국 같은 말이다.)
순수도 or 불순도(엔트로피)
분류 나무는 각 영역 (위의 그림으로 따지자면 하나의 중간 마디 이후 나눠지는 데이터 분류 결과 값)의 순수도가 증가하고 불순도, 불확실성이 감소하도록 학습을 진행한다. 이것을 '정보 획득'이라고도 하는데 쉽게 이해하자면 '순수도 - 1 = 다양성'이라고 볼 수 있고, 다양성이 적을수록 더 높은 점수를 부여하여 모델링하는 것이라 볼 수 있다.
다양성을 낮추는 방향으로 분류
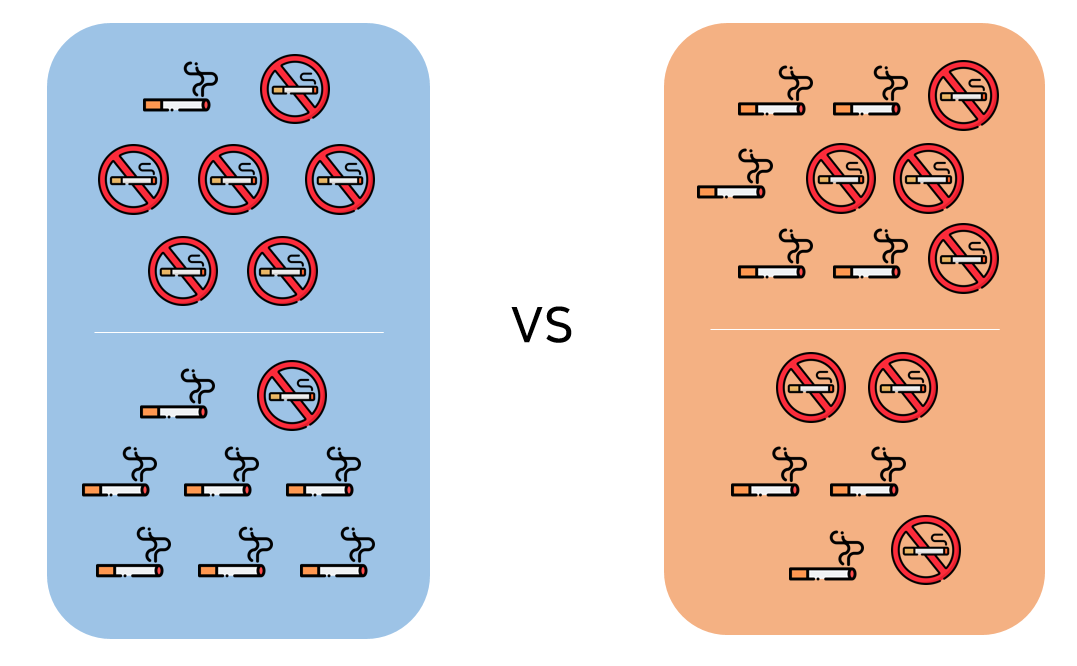
위 그림에 대한 결과로만 살펴보면 왼쪽의 결과가 순수도가 더 높고 다양성이 더 낮다는 것을 알 수 있다. 이 순수도나 불순도를 계산하여 분류에 활용하는데 필요한 지표들이 있다. 대표적으로 사용되고 많이 알려진 두 가지 지표만 살펴보자.
엔트로피
엔트로피는 불확실성을 말한다. 불확실성은 순수도의 반대의 의미로 엔트로피는 낮아질수록 순수도가 높아진다. 때문에 의사결정나무는 엔트로피가 낮아지는 방향으로 학습한다.

$p_k$는 해당 레이블이 나올 확률을 뜻한다. 여기서 확률은 해당 종속변수(담배x, 담배o)가 나타날 '확률'을 뜻하는 것이며 위 예시의 왼쪽(파란색)의 분류 결과를 엔트로피로 나타내게 된다면 다음과 같다.

= $-\frac{1}{7} \log_2 (1/7)$ $-\frac{6}{7} \log_2 (6/7) $
= $-\frac{7}{8} \log_2 (7/8)$ $-\frac{1}{8} \log_2 (1/8)$
로 나타낼 수 있다.
나누기 전의 엔트로피는 흡연X : 7 흡연O: 8 로 0.99의 근사값을 가진다.
\[-\frac{7}{15} \log_2 (7/15) -\frac{8}{15} \log_2 (8/15)) \approx 0.99\]
분류 이후의 엔트로피는 $\frac{7}{15}(-\frac{1}{7} \log_2 (1/7) -\frac{6}{7} \log_2 (6/7)) +\frac{8}{15}( -\frac{7}{8} \log_2 (7/8) -\frac{1}{8} \log_2 (1/8)) \approx 0.57$ 이므로 엔트로피가 0.99 -> 0.57 로 줄어들었다. 즉, 엔트로피가 낮아졌기(= 순수도가 증가) 때문에 분할하는 게 낫다는 결론에 이른다.
또한 오른쪽 분기 후의 결과와 비교했을 때에도 더욱 나은 분할 결과라는 결론을 가진다.

\[\frac{9}{15}(-\frac{5}{9} \log_2 (5/9) -\frac{4}{9} \log_2 (4/9)) +\frac{6}{15}(-\frac{3}{6} \log_2 (3/6) -\frac{3}{6} \log_2 (3/6)) \approx 0.99\]
0.57 < 0.99
지니계수
지니계수도 마찬가지로 불순도를 나타내는 지수. 자주 사용하는 Scikit-learn 라이브러리에서도 '지니계수'를 활용해서 불순도를 측정한다. (CART 알고리즘)


오른쪽, 왼쪽 결과의 각각 분기 후 지니계수를 구해보자.
= $G_1 = 1 - (\frac{1}{7})^2 - (\frac{6}{7})^2 $
: 0.24
= $G_2 = 1 - (\frac{7}{8})^2 - (\frac{1}{8})^2 $
: 0.21
\[\frac{7}{15}G_1+\frac{8}{15}G_2 \approx 0.23\]
마찬가지로 오른쪽 분기 후의 결과와 비교했을 때에도 더 나은 결과라 판단할 수 있다.

= $G_1 = 1 - (\frac{5}{9})^2 - (\frac{4}{9})^2 $
: 0.49
= $G_2 = 1 - (\frac{3}{6})^2 - (\frac{3}{6})^2 $
: 0.5
\[\frac{9}{15}G_1+\frac{6}{15}G_2 \approx 0.49\]
Feature Importance
트리 기반 모델은 트리를 분기하는 과정에서 어떤 변수가 모델에 영향을 많이 주는 '중요한' 변수인지 측정할 수 있다. 이를 통해 각 변수가 얼만큼 분류 모델에 기여했는지에 대한 정보를 전달한다.
import numpy as np
import pandas as pd
import sklearn
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data
label = iris.target
columns = iris.feature_names
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(data, label,
test_size=0.2, shuffle=True, stratify=label, random_state=2019)
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(max_depth=5)
dt.fit(x_train, y_train)
feature_importance = pd.DataFrame(dt.feature_importances_.reshape((1, -1)), columns=columns, index=['feature_importance'])
feature_importance 
sklearn 패키지에서는 의사결정 나무 모델이 지니계수를 사용하는데 각 노드에서 분류작업이 거쳐진 결과들의 불순도(지니계수)를 확인하여 각 변수의 중요도를 측정한다. 즉, 더 순수한 결과를 배출시키는 노드(변수)가 있다면 해당 Feature의 중요도가 올라간다고 할 수 있다.
+) 카디널리티가 높은 변수, 즉 다양한 데이터를 가지고 있는 변수는 중요도를 더욱 부풀릴 가능성이 높다고 한다. 때문에 Feature Importance를 무조건적으로 믿기 보다는 Permutation Feature Importance와 같은 다른 방법도 사용하여 의사결정과 이해에 참고하는 것이 좋다.
참고: 4.2. Permutation feature importance
[머신러닝의 해석] 2편-(1). 트리 기반 모델의 Feature Importance 속성
가지치기
의사결정나무가 간단하고 가독성이 좋다는 장점을 가지고 있지만 트리 구조에 따라서 과대적합이 발생할 가능성이 높다는 단점이 있다. 즉, 분기가 너무 많은 경우 (= 가지가 많은 경우)는 모든 노드의 순도가 100%인 상태를 이야기한다. 너무 세세하게 가지가 나눠져 있어 학습하는 데이터에만 정확도가 높은 Overfitting 현상(과대적합)이 발생할 수 있다. 이러한 문제를 해결하기 위해 적절히 가지를 아래처럼 더 이상 분기하지 않도록 만들어주는 작업이 필요하다.

ratsgo.github.io/machine%20learning/2017/03/26/tree/
과적합을 방지해주기 위한 방법에는 가지치기 이외에도 '앙상블' 방법이 있다. Decision Tree 를 여러 개 두어 모델을 만들어주는 Random Forest 가 앙상블 기법을 활용한 모델이다.
'ML&DL > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Random Forest - 랜덤 포레스트 코드 구현 (feat. python) (0) | 2020.10.04 |
|---|---|
| [Machine Learning] Random Forest - 랜덤 포레스트 (0) | 2020.10.04 |
| [Machine Learning] SVM - 서포트 벡터 머신 (0) | 2020.09.11 |


